Useful Component in Logisim for the Simulation
I/O
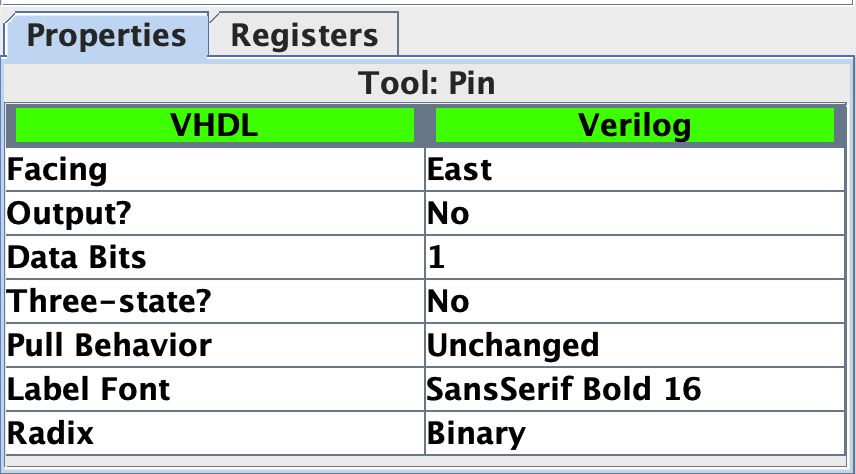
To input or get the output from the circuit, we need to have I/O, and Logisim provides a component called Pin. It has some properties, for example, the Output? property will change the pin between the input mod and the output mod, and the Data Bits property can give us an easy way to input/output multiple bits.
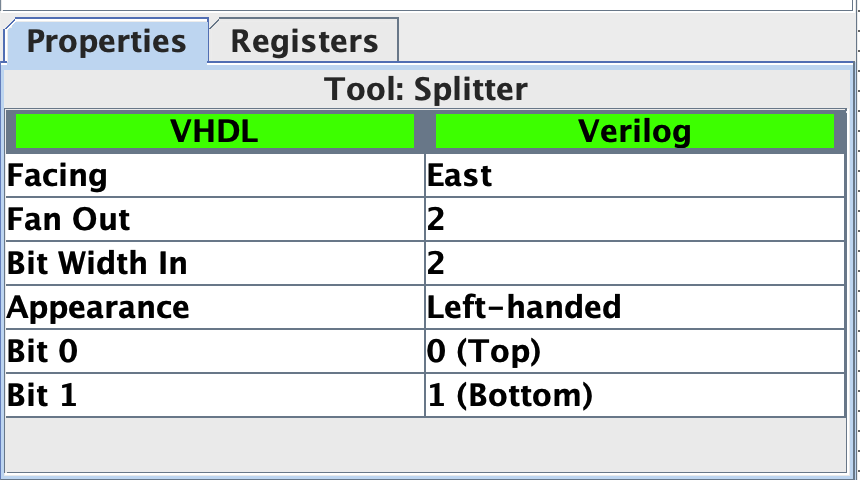
But since one wire can only contain one bit 1/0, when we want to get multiple bits from a pin, we need another component called Splitter. Similar to pin, the splitter also has properties to control the behavior.
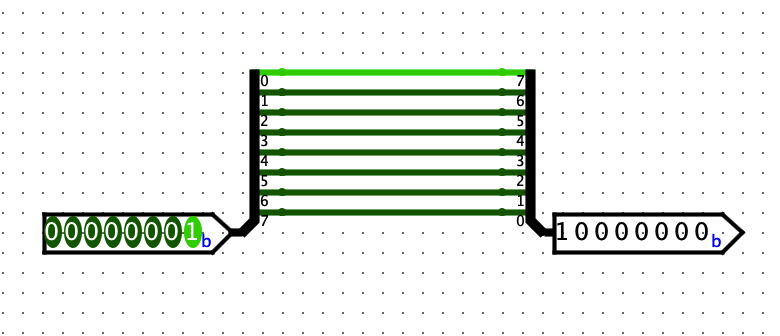
The picture below shows how to get the 8-bit input and then output it in reverse using Pin and Splitter. (The trick is I reversed the bit sequence for the output splitter.)

The picture above is from Export Image function in Logisim, and the picture below is from a direct screenshot. In the following report, I may only paste one of them.
Gates
Logisim provides some logic gates, for me, the most useful gates are not, and, or, xor.
Not Gate

One input and one output, truth table:
| A | Not A |
|---|---|
| T | F |
| F | T |
And Gate
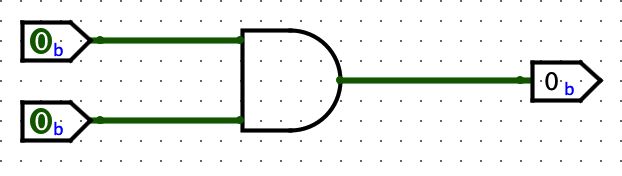
Two inputs and one output, truth table:
| A | B | A and B |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Or Gate
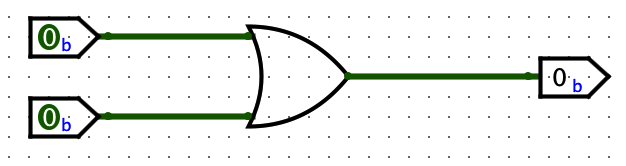
Two inputs and one output, truth table:
| A | B | A or B |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Xor Gate
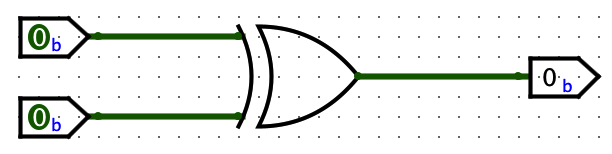
Two inputs and one output, truth table:
| A | B | A xor B |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
The other gate can easily be obtained by combining some of the gates above, e.g., the NAND Gate is an AND Gate with a NOT Gate.
1-Bit Full Adder
Half Adder
Before getting the full adder, let’s only look at 1-bit adding (no carry) in binary:
| A | B | A + B (no carry) |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
If we substitute 1 with T and 0 with F, it’s clear that the table is the same as the XOR truth table. And if we only consider the carry for the 1-bit adding, we can find it’s just an AND operation.
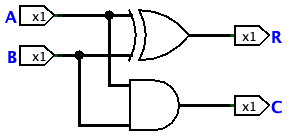
Therefore, the half adder is easy to get, as shown below (A and B are inputs, R stands for the LSB of sum, C stands for the MSB of sum/carry):
Full Adder
After getting the half adder, the next question is how to get the full adder based on it. Firstly, for the full adder, what we actually do is to calculate the A+B+Cin. The intuition tells us the LSB of A+B+Cin is just the no carry sum of the LSB of A+B and Cin, which is R = (A xor B) xor Cin. And for the carry, we can write down the results table and try to find the pattern.
| A+B | Cin | Cout |
|---|---|---|
| 10 | 1 | 1 |
| 10 | 0 | 1 |
| 01 | 1 | 1 |
| 01 | 0 | 0 |
| 00 | 1 | 0 |
| 00 | 0 | 0 |
We can see that the Cout is 1 if and only if either the carry of A+B is 1 or both the LSB of A+B and Cin are 1, which is Cout = (A and B) or (Cin and (A xor B)).
Therefore, the full adder is ready to get, as shown below:
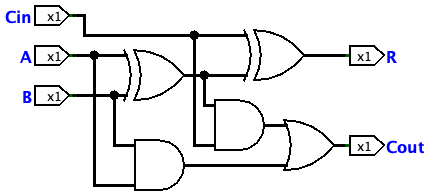
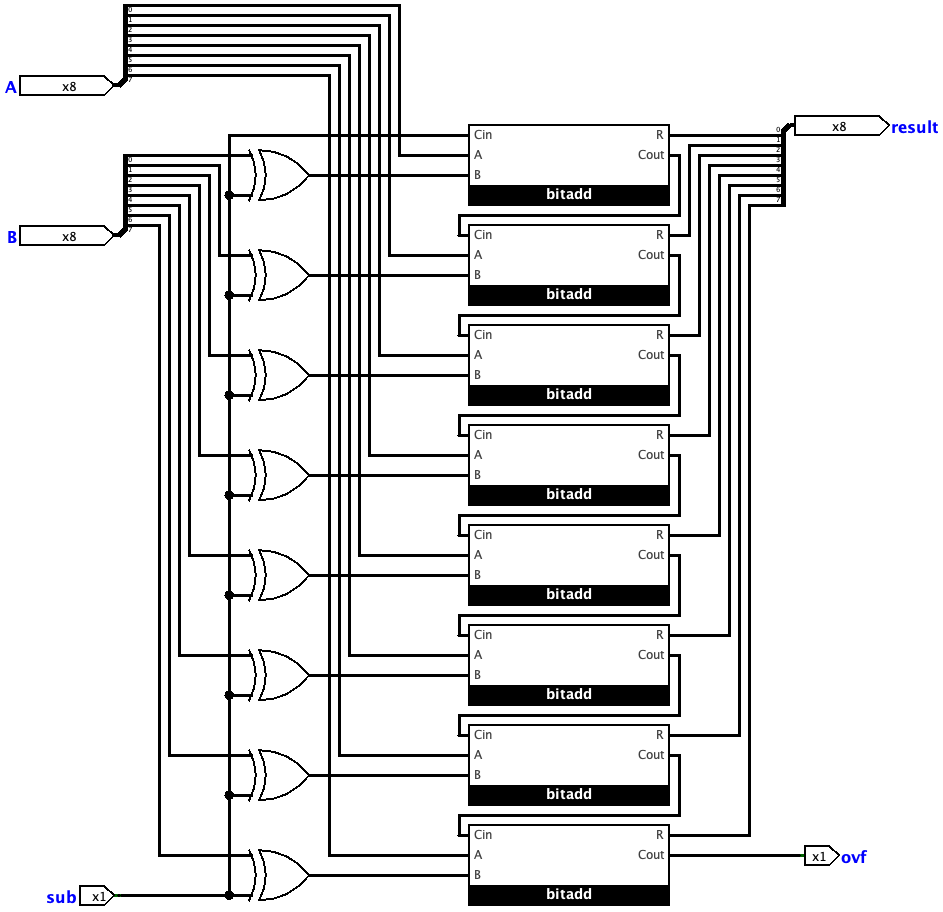
8-Bit Full Adder
From a 1-bit full adder to an 8-bit adder is quite intuitive, just connect every bit of A and B to the corresponding bit adder, and the lower bit’s Cout connects to the higher one’s Cin.
(The bitadd in the picture below is the 1-bit full adder circuit shown above.)
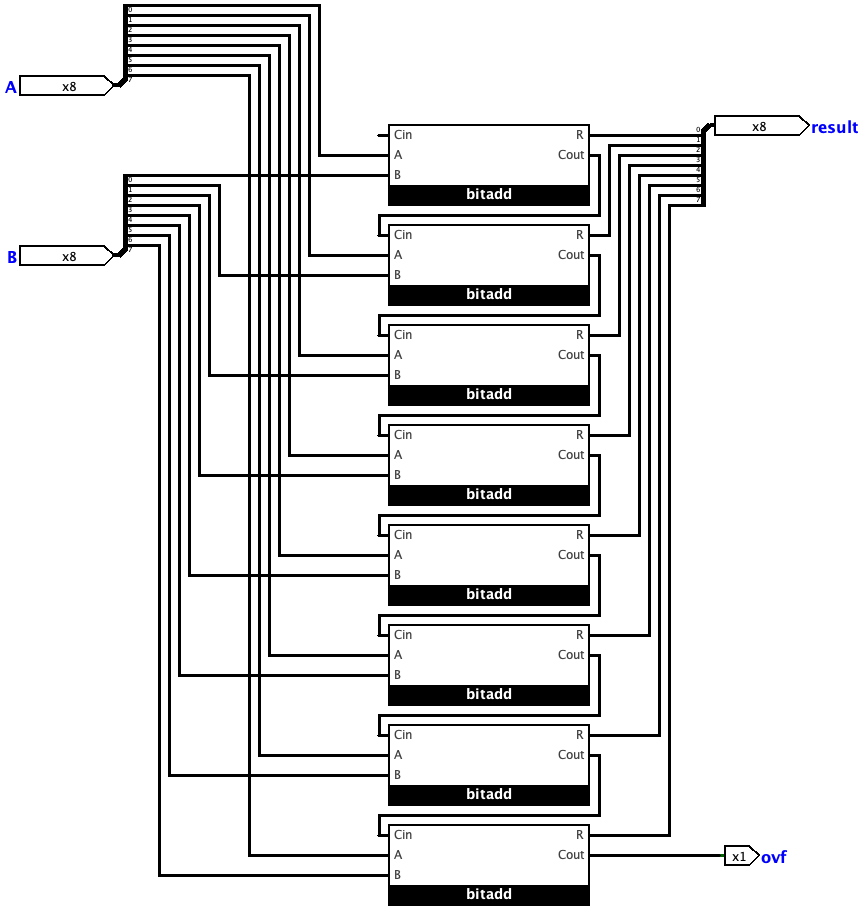
8-Bit Adder/Subtractor
To implement subtraction, we need to know the idea of 2’s complement representation. Simply speaking, to make a number negative, just flip all the bits (0 to 1, 1 to 0) and add 1. In the circuit, what we should do are:
Flip every bit of
Bwhen the sub-signal is1.Add 1 when the sub-signal is
1.
Fortunately, we have a Cin in the LSB bit adder, which can be used for doing the additional add 1 process. But to do the flip, we do need to add some more components/gates. What we want for this gate is when the input of the sub-signal is 1, then flip the input of the B, and when the input of the sub-signal is 0, output the same as from B. We can find that this is just how the XOR gate works.
Therefore, we can get the 8-bit adder/subtractor, as shown below. (In my_adder.circ file, there is another circuit that doesn’t use the bitadd module, but that is too large to put into this report.)