Tree Data Structure

1. Tree Data Structure

Definition of a Tree
- A tree is a data structure that must be connected and contain no circles.
- A single node is a valid tree. A collection of disconnected trees is a “forest”.
- A binary tree is a specific type where each node has at most two children.
Tree Traversal Methods
- Traversal is the process of visiting all nodes in a tree.
- For binary trees, the three common methods are:
  - Pre-order: Node, Left, Right.
  - In-order: Left, Node, Right.
  - Post-order: Left, Right, Node.
- An example:
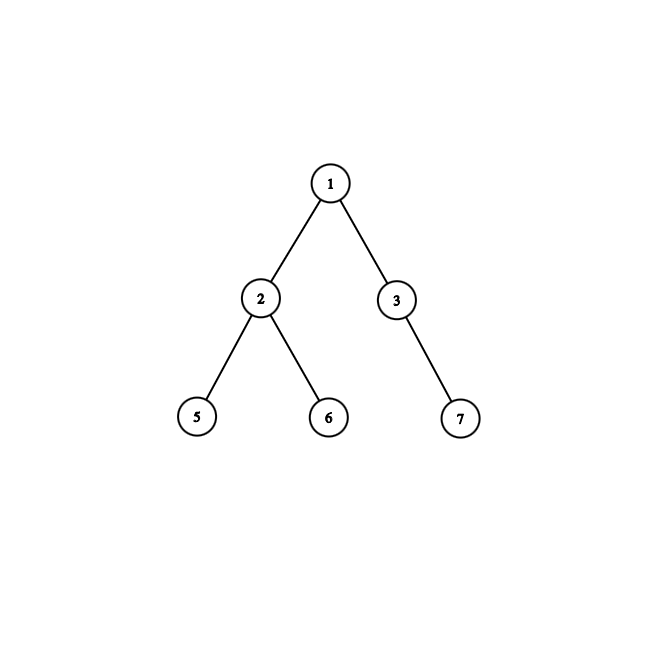
  - Pre-order: 1, 2, 5, 6, 3, 7
  - In-order: 5, 2, 6, 1, 3, 7
  - Post-order: 5, 6, 2, 7, 3, 1

2. Reconstructing a Tree from Traversal Sequences

Uniqueness of Tree Reconstruction
- A single traversal sequence (e.g., pre-order) is not sufficient to uniquely reconstruct a tree.
- A unique tree can be constructed if you are given the in-order sequence and either the pre-order or post-order sequence.
Algorithm for Tree Reconstruction (from Pre-order and In-order)
1. The first element in the pre-order sequence is the root of the current tree/subtree.
2. Locate this root in the in-order sequence.
3. Elements to the left of the root in the in-order sequence form the left subtree; elements to the right form the right subtree.
4. Recursively apply this process to the left and right subtrees using the corresponding segments of the pre-order and in-order sequences.
Code Implementation for Tree Reconstruction (with a tree)

import java.util.*;

class Tree {
    private class Node {
        int val;
        Node lc, rc;

        Node(int val, Node lc, Node rc) {
            this.val = val;
            this.lc = lc;
            this.rc = rc;
        }
    }

    private final Node root;

    private Node buildTree(int[] pre, int[] inOrder, int[] idx,
            int preL, int preR, int inL, int inR) {
        if (preL > preR || inL > inR) {
            return null;
        }

        int cur = pre[preL];
        int cur_idx = idx[cur];
        int left_size = cur_idx - inL;

        Node lc = buildTree(pre, inOrder, idx,
                preL + 1, preL + left_size,
                inL, cur_idx - 1);

        Node rc = buildTree(pre, inOrder, idx,
                preL + left_size + 1, preR,
                cur_idx + 1, inR);

        return new Node(cur, lc, rc);
    }

    private void printPost(Node cur) {
        if (cur == null) {
            return;
        }

        printPost(cur.lc);
        printPost(cur.rc);

        System.out.print(cur.val + " ");
    }

    public void printPost() {
        printPost(root);
    }

    public Tree(int[] pre, int[] inOrder, int[] idx) {
        int n = pre.length;
        root = buildTree(pre, inOrder, idx, 
            0, n - 1, 0, n - 1);
    }
}

public class Traversal {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int t = in.nextInt();
        while (t-- > 0) {
            int n = in.nextInt();
            int[] pre = new int[n];
            int[] inOrder = new int[n];
            int[] idx = new int[n + 1];
            for (int i = 0; i < n; i++) {
                pre[i] = in.nextInt();
            }
            for (int i = 0; i < n; i++) {
                inOrder[i] = in.nextInt();
                idx[inOrder[i]] = i;
            }
            Tree tree = new Tree(pre, inOrder, idx);
            tree.printPost();
            System.out.println();
        }
        in.close();
    }
}

without a tree

import java.util.*;

public class TraversalSim {
    static void dfs(int[] pre, int[] inOrder, int[] idx,
            int preL, int preR, int inL, int inR) {
        if (preL > preR || inL > inR)
            return;

        int cur = pre[preL];
        int cur_idx = idx[cur];
        int left_size = cur_idx - inL;

        dfs(pre, inOrder, idx, 
                preL + 1, preL + left_size, 
                inL, cur_idx - 1);

        dfs(pre, inOrder, idx,
                preL + left_size + 1, preR,
                cur_idx + 1, inR);

        System.out.print(cur + " ");
    }
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int t = in.nextInt();
        while (t-- > 0) {
            int n = in.nextInt();
            int[] pre = new int[n];
            int[] inOrder = new int[n];
            int[] idx = new int[n + 1];
            for (int i = 0; i < n; i++) {
                pre[i] = in.nextInt();
            }
            for (int i = 0; i < n; i++) {
                inOrder[i] = in.nextInt();
                idx[inOrder[i]] = i;
            }
            dfs(pre, inOrder, idx,
                    0, n - 1, 0, n - 1);
            System.out.println();
        }
        in.close();
    }
}

3. Reverse Polish Notation (Postfix Expression)

Expression Trees
- A tree representing a mathematical expression, with operators as internal nodes and operands as leaf nodes.
Postfix Notation (Reverse Polish Notation)
- The sequence obtained by a post-order traversal of an expression tree (e.g., 1 5 6 * + for 1 + 5 * 6).
Evaluating Postfix Expressions with a Stack
- Postfix expressions can be evaluated efficiently in a single pass using a stack.
- Algorithm:
  - Scan the expression from left to right.
  - If an item is an operand (number), push it onto the stack.
  - If an item is an operator, pop the top two operands, perform the operation, and push the result back onto the stack.
- The final result is the only number left on the stack.
Code Implementation for Evaluating RPN

import java.util.*;

public class RPN {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        Stack<Long> st = new Stack<>();

        while (in.hasNext()) {
            String s = in.next();
            if (s.equals("+")) {
                st.push(st.pop() + st.pop());
            } else if (s.equals("-")) {
                long a = st.pop();
                long b = st.pop();
                st.push(b - a);
            } else if (s.equals("*")) {
                st.push(st.pop() * st.pop());
            } else if (s.equals("/")) {
                long a = st.pop();
                long b = st.pop();
                st.push(b / a);
            } else {
                st.push(Long.valueOf(s));
            }
        }

        System.out.println(st.pop());

        in.close();
    }
}

4. Validating a Binary Search Tree (BST)

Definition of a BST
- A tree where a node’s value is greater than all values in its left subtree and smaller than all values in its right subtree.
Solution 1: In-order Traversal
- A key property of a valid BST is that its in-order traversal results in a strictly increasing sequence. This can be used for validation.
Solution 2: Recursive Traversal with Bounds
- The recursive approach passes down an upper and lower bound for each node to validate against.
- For a left child, the upper bound becomes the parent’s value.
- For a right child, the lower bound becomes the parent’s value.
Code Implementation for Validating BST by Recursion

import java.util.*;

class Tree {
    private class Node {
        final int val;
        final int lc, rc;
        Node(int val, int lc, int rc) {
            this.val = val;
            this.lc = lc;
            this.rc = rc;
        }
    }

    Node[] nodes;

    public void iaddNode(int idx, int val, int l, int r) {
        nodes[idx] = new Node(val, l, r);
    }

    public Tree(int n) {
        nodes = new Node[n + 1];
        nodes[0] = null;
    }

    private boolean isValid(Node cur, int min, int max) {
        if (cur == null)
            return true;
        if (cur.val <= min || cur.val >= max)
            return false;

        return isValid(nodes[cur.lc], min, cur.val) 
            && isValid(nodes[cur.rc], cur.val, max);
    }

    public boolean isValid() {
        return isValid(nodes[1], Integer.MIN_VALUE, Integer.MAX_VALUE);
    }
}

public class validBst {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int t = in.nextInt();
        while (t-- > 0) {
            int n = in.nextInt();
            Tree tree = new Tree(n);
            for (int i = 1; i <= n; i++) {
                int v, l, r;
                v = in.nextInt();
                l = in.nextInt();
                r = in.nextInt();
                tree.iaddNode(i, v, l, r);
            }

            if (tree.isValid()) {
                System.out.println("YES");
            } else {
                System.out.println("NO");
            }
        }
        in.close();
    }
}

5. Finding a Dynamic Cut-off Score

Problem Description
- Dynamically find the score of the $T$-th ranked student from a list of scores as new scores are added and $T$ changes.
Proposed Solution: Two Heaps
- Min-Heap (“winners”): Stores the top $T$ scores. Its root is the cut-off score.
- Max-Heap (“others”): Stores all other scores.
Logic of the Two-Heap Algorithm
1. Add New Score: When a new score arrives, place it in the appropriate heap by comparing it to the current cut-off score (root of the min-heap).
2. Adjust Heaps: Move elements between the heaps until the “winners” min-heap has exactly $T$ elements.
3. Get Result: The root of the “winners” min-heap is always the current cut-off score.
Small Trick for Max-Heap
- In Java, a max-heap can be created from a PriorityQueue using Collections.reverseOrder() or by storing the negative of each value in a standard min-heap.
Code Implementation for the Problem

import java.util.*;

public class Awards {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int w = in.nextInt();
        PriorityQueue<Integer> winner = new PriorityQueue<>();
        PriorityQueue<Integer> others = 
            new PriorityQueue<>(Collections.reverseOrder());

        for (int i = 0; i < n; i++) {
            int score = in.nextInt();
            int planWin = (int) Math.max(1, (1l * (i + 1) * w) / 100);

            if (winner.isEmpty()) {
                others.add(score);
            } else {
                int smallest = winner.peek();
                if (score > smallest) {
                    others.add(winner.poll());
                    winner.add(score);
                } else {
                    others.add(score);
                }
            }

            while (winner.size() < planWin) {
                winner.add(others.poll());
            }

            System.out.print(winner.peek() + " ");
        }

        in.close();
    }
}

1. Tree Data Structure#

2. Reconstructing a Tree from Traversal Sequences#

3. Reverse Polish Notation (Postfix Expression)#

4. Validating a Binary Search Tree (BST)#

5. Finding a Dynamic Cut-off Score#

1. Tree Data Structure

2. Reconstructing a Tree from Traversal Sequences

3. Reverse Polish Notation (Postfix Expression)

4. Validating a Binary Search Tree (BST)

5. Finding a Dynamic Cut-off Score